The article, Analyzing Data 180,000x Faster with Rust, first presents some unoptimized Python code, and then shows the process of rewriting and optimizing the code in Rust, resulting in a 180,000x speed-up. The author notes:
There are lots of ways we could make the Python code faster, but the point of this post isn’t to compare highly-optimized Python to highly-optimized Rust. The point is to compare “standard-Jupyter-notebook” Python to highly-optimized Rust.
The question arises: if we were to stick with Python, what kind of speed-ups could we achieve?
In this post, we will go through a journey of profiling and iteratively speeding up the code, in Python.
Replicating the original benchmarks
The times in this post are comparable to the times reported in the original article. Using a similar computer (M1 Macbook Pro), I measure:
- 35 ms average iteration time for the original unoptimized code, measured over 1,000 iterations. The original article reports 36 ms.
- 180,081x speedup, for the fully optimized Rust code, measured over 5,000,000 iterations. The original article reports 182,450x.
Python Baseline
Here is a replication of the baseline, unoptimized Python code, from the article.
from itertools import combinations
import pandas as pd
from pandas import IndexSlice as islice
def k_corrset(data, K):
all_qs = data.question.unique()
q_to_score = data.set_index(['question', 'user'])
all_grand_totals = data.groupby('user').score.sum().rename('grand_total')
# Inner loop
corrs = []
for qs in combinations(all_qs, K):
qs_data = q_to_score.loc[islice[qs,:],:].swaplevel()
answered_all = qs_data.groupby(level=[0]).size() == K
answered_all = answered_all[answered_all].index
qs_totals = qs_data.loc[islice[answered_all,:]] \
.groupby(level=[0]).sum().rename(columns={'score': 'qs'})
r = qs_totals.join(all_grand_totals).corr().qs.grand_total
corrs.append({'qs': qs, 'r': r})
corrs = pd.DataFrame(corrs)
return corrs.sort_values('r', ascending=False).iloc[0].qs
data = pd.read_json('scores.json')
print(k_corrset(data, K=5))
And here are the first two rows of the dataframe, data.
| user |
question |
score |
| e213cc2b-387e-4d7d-983c-8abc19a586b1 |
d3bdb068-7245-4521-ae57-d0e9692cb627 |
1 |
| 951ffaee-6e17-4599-a8c0-9dfd00470cd9 |
d3bdb068-7245-4521-ae57-d0e9692cb627 |
0 |
We can use the output from the original code to test the correctness of our optimized code.
Since we are trying to optimize the the inner loop, let’s put the inner loop into its own function, to profile it using line_profiler.
Avg time per iteration: 35 ms
Speedup over baseline: 1.0x
% Time Line Contents
=====================
def compute_corrs(
qs_iter: Iterable, q_to_score: pd.DataFrame, grand_totals: pd.DataFrame
):
0.0 result = []
0.0 for qs in qs_iter:
13.5 qs_data = q_to_score.loc[islice[qs, :], :].swaplevel()
70.1 answered_all = qs_data.groupby(level=[0]).size() == K
0.4 answered_all = answered_all[answered_all].index
0.0 qs_total = (
6.7 qs_data.loc[islice[answered_all, :]]
1.1 .groupby(level=[0])
0.6 .sum()
0.3 .rename(columns={"score": "qs"})
)
7.4 r = qs_total.join(grand_totals).corr().qs.grand_total
0.0 result.append({"qs": qs, "r": r})
0.0 return result
We can see the value we are trying to optimize, (the average iteration time / speedup), as well as the proportion of time spent on each line.
This lends itself to the following workflow for optimizing the code:
- Run the profiler
- Identify the slowest lines
- Try make to the slower lines faster
- Test the output for correctness, (important)
- Repeat
If there are just a few lines taking up the majority of the time, we know what to focus on — e.g. in the above code block we see that there is a particularly slow line, taking up ~70% of the time.
While working on this, I created a helper function that ran both profiling and tests; this enabled me to try things out and get measurements while ensuring that the code was still valid.
Optimization 1 - dictionary of sets of users who answered questions, users_who_answered_q
The baseline carries out various heavy Pandas operations, to find out which users answered the current set of questions, qs. In particular, it checks every row of the dataframe to find out which users answered the questions. For the first optimization, instead of using the full dataframe, we can use a dictionary of sets. This lets us quickly look up which users answered each question in qs, and use Python’s set intersection to find out which users anwered all of the questions.
Avg time per iteration: 10.0 ms
Speedup over baseline: 3.5x
% Time Line Contents
=====================
def compute_corrs(qs_iter, users_who_answered_q, q_to_score, grand_totals):
0.0 result = []
0.0 for qs in qs_iter:
0.0 user_sets_for_qs = [users_who_answered_q[q] for q in qs]
3.6 answered_all = set.intersection(*user_sets_for_qs)
40.8 qs_data = q_to_score.loc[islice[qs, :], :].swaplevel()
0.0 qs_total = (
22.1 qs_data.loc[islice[list(answered_all), :]]
3.7 .groupby(level=[0])
1.9 .sum()
1.1 .rename(columns={"score": "qs"})
)
26.8 r = qs_total.join(grand_totals).corr().qs.grand_total
0.0 result.append({"qs": qs, "r": r})
0.0 return result
This significantly speeds up the lines that compute, answered_all, which have gone from taking up 70% of the time, to 4%, and we are already over 3x faster than the baseline.
Optimization 2 - score_dict dictionary
If we add up the amount of time spent on each line that contributes to computing qs_total, (including the qs_data line), it comes to ~65%; so the next thing to optimize is clear. We can again switch out heavy operations on the full dataset, (indexing, grouping, etc.) with fast dictionary look ups. We introduce score_dict, a dictionary that lets us look up the score for a given question and user pair.
Avg time per iteration: 690 μs
Speedup over baseline: 50.8x
% Time Line Contents
=====================
def compute_corrs(qs_iter, users_who_answered_q, score_dict, grand_totals):
0.0 result = []
0.0 for qs in qs_iter:
0.1 user_sets_for_qs = [users_who_answered_q[q] for q in qs]
35.9 answered_all = set.intersection(*user_sets_for_qs)
3.4 qs_total = {u: sum(score_dict[q, u] for q in qs) for u in answered_all}
8.6 qs_total = pd.DataFrame.from_dict(qs_total, orient="index", columns=["qs"])
0.1 qs_total.index.name = "user"
51.8 r = qs_total.join(grand_totals).corr().qs.grand_total
0.0 result.append({"qs": qs, "r": r})
0.0 return result
This gives us a nice 50x speed up.
Optimization 3 - grand_totals dictionary, and np.corrcoef
The slowest line above does multiple things, it does a Pandas join, to combine the grand_totals, with the qs_total, and then it computes the correlation coefficient for this. Again, we can speed this up by using a dictionary lookup instead of a join, and since we no longer have Pandas objects, we use np.corrcoef instead of Pandas corr.
Avg time per iteration: 380 μs
Speedup over baseline: 91.6x
% Time Line Contents
=====================
def compute_corrs(qs_iter, users_who_answered_q, score_dict, grand_totals):
0.0 result = []
0.0 for qs in qs_iter:
0.2 user_sets_for_qs = [users_who_answered_q[q] for q in qs]
83.9 answered_all = set.intersection(*user_sets_for_qs)
7.2 qs_total = [sum(score_dict[q, u] for q in qs) for u in answered_all]
0.5 user_grand_total = [grand_totals[u] for u in answered_all]
8.1 r = np.corrcoef(qs_total, user_grand_total)[0, 1]
0.1 result.append({"qs": qs, "r": r})
0.0 return result
This gives us a ~90x speedup.
Optimization 4 - uuid strings to ints
The next optimization doesn’t alter the code in the inner loop at all. But it does speed up some of the operations. We replace the long user/question uuids, (e.g. e213cc2b-387e-4d7d-983c-8abc19a586b1), with, much shorter, ints. How it’s done:
data.user = data.user.map({u: i for i, u in enumerate(data.user.unique())})
data.question = data.question.map(
{q: i for i, q in enumerate(data.question.unique())}
)
And we measure:
Avg time per iteration: 210 μs
Speedup over baseline: 168.5x
% Time Line Contents
=====================
def compute_corrs(qs_iter, users_who_answered_q, score_dict, grand_totals):
0.0 result = []
0.1 for qs in qs_iter:
0.4 user_sets_for_qs = [users_who_answered_q[q] for q in qs]
71.6 answered_all = set.intersection(*user_sets_for_qs)
13.1 qs_total = [sum(score_dict[q, u] for q in qs) for u in answered_all]
0.9 user_grand_total = [grand_totals[u] for u in answered_all]
13.9 r = np.corrcoef(qs_total, user_grand_total)[0, 1]
0.1 result.append({"qs": qs, "r": r})
0.0 return result
Optimization 5 - np.bool_ array instead of sets of users
We can see that the set operation above is still the slowest line. Instead of using sets of ints, we switch to using a np.bool_ array of users, and use np.logical_and.reduce to find the users that answered all of the questions in qs. (Note that np.bool_ uses a whole byte for each element, but np.logical_and.reduce is still pretty fast.) This gives a signicant speedup:
Avg time per iteration: 75 μs
Speedup over baseline: 466.7x
% Time Line Contents
=====================
def compute_corrs(qs_iter, users_who_answered_q, score_dict, grand_totals):
0.0 result = []
0.1 for qs in qs_iter:
12.0 user_sets_for_qs = users_who_answered_q[qs, :] # numpy indexing
9.9 answered_all = np.logical_and.reduce(user_sets_for_qs)
10.7 answered_all = np.where(answered_all)[0]
33.7 qs_total = [sum(score_dict[q, u] for q in qs) for u in answered_all]
2.6 user_grand_total = [grand_totals[u] for u in answered_all]
30.6 r = np.corrcoef(qs_total, user_grand_total)[0, 1]
0.2 result.append({"qs": qs, "r": r})
0.0 return result
Optimization 6 - score_matrix instead of dict
The slowest line above is now the computation of qs_total. Following the example of the original article, we switch to using a dense np.array to look up the scores, instead of a dictionary, and use fast NumPy indexing to get the scores.
Avg time per iteration: 56 μs
Speedup over baseline: 623.7x
% Time Line Contents
=====================
def compute_corrs(qs_iter, users_who_answered_q, score_matrix, grand_totals):
0.0 result = []
0.2 for qs in qs_iter:
16.6 user_sets_for_qs = users_who_answered_q[qs, :]
14.0 answered_all = np.logical_and.reduce(user_sets_for_qs)
14.6 answered_all = np.where(answered_all)[0]
7.6 qs_total = score_matrix[answered_all, :][:, qs].sum(axis=1)
3.9 user_grand_total = [grand_totals[u] for u in answered_all]
42.7 r = np.corrcoef(qs_total, user_grand_total)[0, 1]
0.4 result.append({"qs": qs, "r": r})
0.0 return result
Optimization 7 - custom corrcoef
The slowest line above is np.corrcoef… We will do what it takes to optimize our code, so here’s our own corrcoef implementation, that’s twice as fast for this use case:
def corrcoef(a: list[float], b: list[float]) -> float | None:
"""same as np.corrcoef(a, b)[0, 1]"""
n = len(a)
sum_a = sum(a)
sum_b = sum(b)
sum_ab = sum(a_i * b_i for a_i, b_i in zip(a, b))
sum_a_sq = sum(a_i**2 for a_i in a)
sum_b_sq = sum(b_i**2 for b_i in b)
num = n * sum_ab - sum_a * sum_b
den = sqrt(n * sum_a_sq - sum_a**2) * sqrt(n * sum_b_sq - sum_b**2)
if den == 0:
return None
return num / den
And we get a decent speed up:
Avg time per iteration: 43 μs
Speedup over baseline: 814.6x
% Time Line Contents
=====================
def compute_corrs(qs_iter, users_who_answered_q, score_matrix, grand_totals):
0.0 result = []
0.2 for qs in qs_iter:
21.5 user_sets_for_qs = users_who_answered_q[qs, :] # numpy indexing
18.7 answered_all = np.logical_and.reduce(user_sets_for_qs)
19.7 answered_all = np.where(answered_all)[0]
10.0 qs_total = score_matrix[answered_all, :][:, qs].sum(axis=1)
5.3 user_grand_total = [grand_totals[u] for u in answered_all]
24.1 r = corrcoef(qs_total, user_grand_total)
0.5 result.append({"qs": qs, "r": r})
0.0 return result
Optimization 8 - Premature introduction of Numba
We haven’t finished optimizing the data structures in the code above, but let’s see what would happen if we were to introduce Numba at this stage. Numba is a library in the Python ecosystem that “translates a subset of Python and NumPy code into fast machine code”.
In order to be able to use Numba, we make two changes:
Modification 1: Pass qs_combinations as numpy array, instead of qs_iter
Numba doesn’t play well with itertools or generators, so we turn qs_iter into a NumPy array in advance, to give to the function. The impact of this change on the time, (before adding Numba), is shown below.
Avg time per iteration: 42 μs
Speedup over baseline: 829.2x
Modification 2: Result array instead of list
Rather than appending to a list, we initialise an array, and put the results in it. The impact of this change on the time, (before adding Numba), is shown below.
Avg time per iteration: 42 μs
Speedup over baseline: 833.8x
The code ends up looking like this:
import numba
@numba.njit(parallel=False)
def compute_corrs(qs_combinations, users_who_answered_q, score_matrix, grand_totals):
result = np.empty(len(qs_combinations), dtype=np.float64)
for i in numba.prange(len(qs_combinations)):
qs = qs_combinations[i]
user_sets_for_qs = users_who_answered_q[qs, :]
# numba doesn't support np.logical_and.reduce
answered_all = user_sets_for_qs[0]
for j in range(1, len(user_sets_for_qs)):
answered_all *= user_sets_for_qs[j]
answered_all = np.where(answered_all)[0]
qs_total = score_matrix[answered_all, :][:, qs].sum(axis=1)
user_grand_total = grand_totals[answered_all]
result[i] = corrcoef_numba(qs_total, user_grand_total)
return result
(Note that we also decorated corrcoef with Numba, because the functions called within a Numba function also need to have been compiled.)
Results, with parallel=False
Avg time per iteration: 47 μs
Speedup over baseline: 742.2x
Results, with parallel=True
Avg time per iteration: 8.5 μs
Speedup over baseline: 4142.0x
We see that with parallel=False the Numba code is slightly slower than the previous Python code, but when we turn on the parallelism, we start making use of all of our CPU cores (10 on the machine running the benchmarks), which gives a good speed multiplier.
However, we lose the ability to use line_profiler, on the JIT compiled code; (we might want to start looking at the generated LLVM IR / assembly).
Optimization 9 - Bitsets, no Numba
Let’s put Numba aside for now. The original article uses bitsets to quickly compute the users who answered the current qs, so let’s see if that will work for us. We can use NumPy arrays of np.int64, and np.bitwise_and.reduce, to implement bitsets. This is different from the np.bool_ array we used before, because we are now using the individual bits within a byte, to represent the entities within a set. Note that we might need multiple bytes for a given bitset, depending on the max number of elements that we need. We can use fast bitwise_and on the bytes of each question in qs to find the set intersection, and therefore the number of users who answered all the qs.
Here are the bitset functions we’ll use:
def bitset_create(size):
"""Initialise an empty bitset"""
size_in_int64 = int(np.ceil(size / 64))
return np.zeros(size_in_int64, dtype=np.int64)
def bitset_add(arr, pos):
"""Add an element to a bitset"""
int64_idx = pos // 64
pos_in_int64 = pos % 64
arr[int64_idx] |= np.int64(1) << np.int64(pos_in_int64)
def bitset_to_list(arr):
"""Convert a bitset back into a list of ints"""
result = []
for idx in range(arr.shape[0]):
if arr[idx] == 0:
continue
for pos in range(64):
if (arr[idx] & (np.int64(1) << np.int64(pos))) != 0:
result.append(idx * 64 + pos)
return np.array(result)
And we can initialize the bitsets as follows:
users_who_answered_q = np.array(
[bitset_create(data.user.nunique()) for _ in range(data.question.nunique())]
)
for q, u in data[["question", "user"]].values:
bitset_add(users_who_answered_q[q], u)
Let’s see the speedup we get:
Avg time per iteration: 550 μs
Speedup over baseline: 64.2x
% Time Line Contents
=====================
def compute_corrs(qs_combinations, users_who_answered_q, score_matrix, grand_totals):
0.0 num_qs = qs_combinations.shape[0]
0.0 bitset_size = users_who_answered_q[0].shape[0]
0.0 result = np.empty(qs_combinations.shape[0], dtype=np.float64)
0.0 for i in range(num_qs):
0.0 qs = qs_combinations[i]
0.3 user_sets_for_qs = users_who_answered_q[qs_combinations[i]]
0.4 answered_all = np.bitwise_and.reduce(user_sets_for_qs)
96.7 answered_all = bitset_to_list(answered_all)
0.6 qs_total = score_matrix[answered_all, :][:, qs].sum(axis=1)
0.0 user_grand_total = grand_totals[answered_all]
1.9 result[i] = corrcoef(qs_total, user_grand_total)
0.0 return result
It looks like we’ve regressed somewhat, with the bitset_to_list operation taking up a lot of time.
Optimization 10 - Numba on bitset_to_list
Let’s convert bitset_to_list into compiled code. To do this we can add a Numba decorator:
@numba.njit
def bitset_to_list(arr):
result = []
for idx in range(arr.shape[0]):
if arr[idx] == 0:
continue
for pos in range(64):
if (arr[idx] & (np.int64(1) << np.int64(pos))) != 0:
result.append(idx * 64 + pos)
return np.array(result)
And let’s measure this:
Benchmark #14: bitsets, with numba on bitset_to_list
Using 1000 iterations...
Avg time per iteration: 19 μs
Speedup over baseline: 1801.2x
% Time Line Contents
=====================
def compute_corrs(qs_combinations, users_who_answered_q, score_matrix, grand_totals):
0.0 num_qs = qs_combinations.shape[0]
0.0 bitset_size = users_who_answered_q[0].shape[0]
0.0 result = np.empty(qs_combinations.shape[0], dtype=np.float64)
0.3 for i in range(num_qs):
0.6 qs = qs_combinations[i]
8.1 user_sets_for_qs = users_who_answered_q[qs_combinations[i]]
11.8 answered_all = np.bitwise_and.reduce(user_sets_for_qs)
7.7 answered_all = bitset_to_list(answered_all)
16.2 qs_total = score_matrix[answered_all, :][:, qs].sum(axis=1)
1.1 user_grand_total = grand_totals[answered_all]
54.1 result[i] = corrcoef(qs_total, user_grand_total)
0.0 return result
We’ve got an 1,800x speed up over the original code. Recall that optimization 7, before Numba was introduced, got 814x. (Optimization 8 got 4142x, but that was with parallel=True on the inner loop, so it’s not comparible to the above.)
Optimization 11 - Numba on corrcoef
The corrcoef line is again standing out as slow above. Let’s use corrcoef decorated with Numba.
@numba.njit
def corrcoef_numba(a, b):
"""same as np.corrcoef(a, b)[0, 1]"""
n = len(a)
sum_a = sum(a)
sum_b = sum(b)
sum_ab = sum(a * b)
sum_a_sq = sum(a * a)
sum_b_sq = sum(b * b)
num = n * sum_ab - sum_a * sum_b
den = math.sqrt(n * sum_a_sq - sum_a**2) * math.sqrt(n * sum_b_sq - sum_b**2)
return np.nan if den == 0 else num / den
And benchmark:
Avg time per iteration: 11 μs
Speedup over baseline: 3218.9x
% Time Line Contents
=====================
def compute_corrs(qs_combinations, users_who_answered_q, score_matrix, grand_totals):
0.0 num_qs = qs_combinations.shape[0]
0.0 bitset_size = users_who_answered_q[0].shape[0]
0.0 result = np.empty(qs_combinations.shape[0], dtype=np.float64)
0.7 for i in range(num_qs):
1.5 qs = qs_combinations[i]
15.9 user_sets_for_qs = users_who_answered_q[qs_combinations[i]]
26.1 answered_all = np.bitwise_and.reduce(user_sets_for_qs)
16.1 answered_all = bitset_to_list(answered_all)
33.3 qs_total = score_matrix[answered_all, :][:, qs].sum(axis=1)
2.0 user_grand_total = grand_totals[answered_all]
4.5 result[i] = corrcoef_numba(qs_total, user_grand_total)
0.0 return result
Nice, another big speedup.
Optimization 12 - Numba on bitset_and
Instead of using np.bitwise_and.reduce, we introduce bitwise_and, and jit compile it.
@numba.njit
def bitset_and(arrays):
result = arrays[0].copy()
for i in range(1, len(arrays)):
result &= arrays[i]
return result
Benchmark #16: numba also on bitset_and
Using 1000 iterations...
Avg time per iteration: 8.9 μs
Speedup over baseline: 3956.7x
% Time Line Contents
=====================
def compute_corrs(qs_combinations, users_who_answered_q, score_matrix, grand_totals):
0.1 num_qs = qs_combinations.shape[0]
0.0 bitset_size = users_who_answered_q[0].shape[0]
0.1 result = np.empty(qs_combinations.shape[0], dtype=np.float64)
1.0 for i in range(num_qs):
1.5 qs = qs_combinations[i]
18.4 user_sets_for_qs = users_who_answered_q[qs_combinations[i]]
16.1 answered_all = bitset_and(user_sets_for_qs)
17.9 answered_all = bitset_to_list(answered_all)
37.8 qs_total = score_matrix[answered_all, :][:, qs].sum(axis=1)
2.4 user_grand_total = grand_totals[answered_all]
4.8 result[i] = corrcoef_numba(qs_total, user_grand_total)
0.0 return result
Optimization 13 - Numba on the whole function
The above is now considerably faster than the original code, with the computation spread fairly evenly out among a few lines in the loop. In fact, it looks like the slowest line is carrying out NumPy indexing, which is already pretty fast. So, let’s compile the whole function with Numba.
@numba.njit(parallel=False)
def compute_corrs(qs_combinations, users_who_answered_q, score_matrix, grand_totals):
result = np.empty(len(qs_combinations), dtype=np.float64)
for i in numba.prange(len(qs_combinations)):
qs = qs_combinations[i]
user_sets_for_qs = users_who_answered_q[qs, :]
answered_all = user_sets_for_qs[0]
# numba doesn't support np.logical_and.reduce
for j in range(1, len(user_sets_for_qs)):
answered_all *= user_sets_for_qs[j]
answered_all = np.where(answered_all)[0]
qs_total = score_matrix[answered_all, :][:, qs].sum(axis=1)
user_grand_total = grand_totals[answered_all]
result[i] = corrcoef_numba(qs_total, user_grand_total)
return result
Avg time per iteration: 4.2 μs
Speedup over baseline: 8353.2x
And now with parallel=True:
Avg time per iteration: 960 ns
Speedup over baseline: 36721.4x
Ok, nice we are 36,000 times faster than the original code.
Optimization 14 - Numba, inline with accumulation instead of arrays
Where do we go from here?… Well, in the code above there’s still a fair amount of putting values into arrays, and then passing them around. Since we are are making the effort to optimize this code, we can look at the way corrcoef is computed, and realise that we don’t need to build up the arrays answered_all, and user_grand_total, we can instead accumulate the values, as we loop.
And here’s the code (we’ve also enabled some compiler optimizations, like disabling boundschecking of arrays, and enabling fastmath).
@numba.njit(boundscheck=False, fastmath=True, parallel=False, nogil=True)
def compute_corrs(qs_combinations, users_who_answered_q, score_matrix, grand_totals):
num_qs = qs_combinations.shape[0]
bitset_size = users_who_answered_q[0].shape[0]
corrs = np.empty(qs_combinations.shape[0], dtype=np.float64)
for i in numba.prange(num_qs):
# bitset will contain users who answered all questions in qs_array[i]
bitset = users_who_answered_q[qs_combinations[i, 0]].copy()
for q in qs_combinations[i, 1:]:
bitset &= users_who_answered_q[q]
# retrieve stats for the users to compute correlation
n = 0.0
sum_a = 0.0
sum_b = 0.0
sum_ab = 0.0
sum_a_sq = 0.0
sum_b_sq = 0.0
for idx in range(bitset_size):
if bitset[idx] != 0:
for pos in range(64):
if (bitset[idx] & (np.int64(1) << np.int64(pos))) != 0:
user_idx = idx * 64 + pos
score_for_qs = 0.0
for q in qs_combinations[i]:
score_for_qs += score_matrix[user_idx, q]
score_for_user = grand_totals[user_idx]
n += 1.0
sum_a += score_for_qs
sum_b += score_for_user
sum_ab += score_for_qs * score_for_user
sum_a_sq += score_for_qs * score_for_qs
sum_b_sq += score_for_user * score_for_user
num = n * sum_ab - sum_a * sum_b
den = np.sqrt(n * sum_a_sq - sum_a**2) * np.sqrt(n * sum_b_sq - sum_b**2)
corrs[i] = np.nan if den == 0 else num / den
return corrs
We start with parallel=False.
Avg time per iteration: 1.7 μs
Speedup over baseline: 20850.5x
This should be compared to optimization 12 with parallel=False, which measured as 8353x.
Now, with parallel=True.
Avg time per iteration: 210 ns
Speedup over baseline: 170476.3x
Nice, we’ve got to 170,000x the speed of the Python baseline.
Conclusion
We’ve been able to get most of the things that made the optimized Rust code fast, notably, bitsets, SIMD, and loop-level parallelism, thanks to Numba and NumPy. First, we made the original Python code considerably faster, with a few helper functions JIT compiled, but in the end we JITed the whole thing, and optimized the code for that. We took a trial and improvement approach, using profiling to focus our efforts on the slowest lines of code. We showed that we can use Numba to gradually mix JIT compiled code into our Python codebase. We can drop this code into our existing Python codebase immediately. However, we didn’t get to the 180,000x speed up of the optimized Rust code, and we rolled our own correlation and bitsets implementation, whereas the Rust code was able to use libraries for these, while remaining fast.
This was a fun exercise, that hopefully shows off some useful tools in the Python ecosystem.
Would I recommend one approach over the other? No, it depends on the situation.
Notes
The full code is here, on GitHub.
]]>
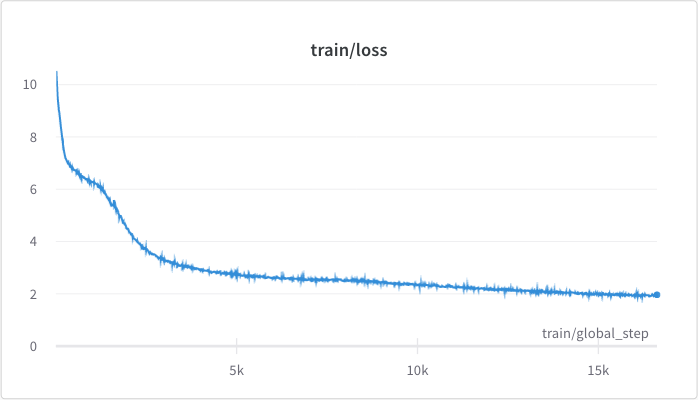<figcaption>The pre-training loss.</figcaption>
).](/assets/posts/bert-from-scratch/learning_rate.png)
<figcaption>The learning rate schedule, recommended by Cramming (Geiping et al, 2022).</figcaption>
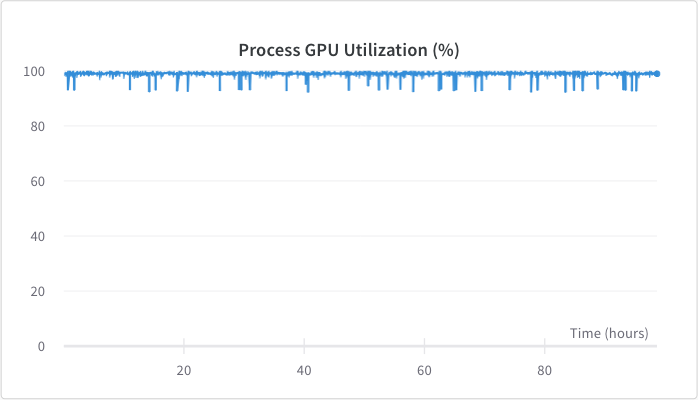<figcaption>GPU utilization was around 98%.</figcaption>
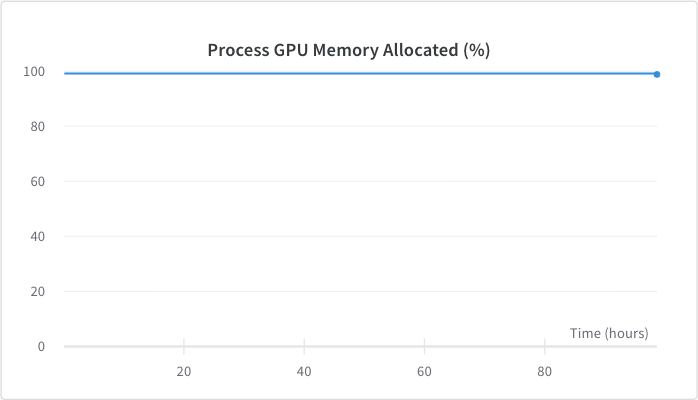<figcaption>GPU memory usage was around 98%, this was achieved by adjusting the batch size.</figcaption>
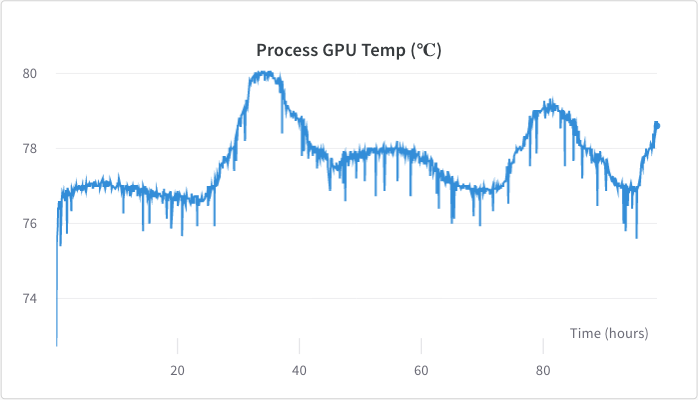<figcaption>GPU temperature stayed between 76 - 80 degrees celsius, with a higher temperature on hotter days.</figcaption>