Measuring the learning per example, via loss diffs
This post introduces the concept of the learning per example (LPE). LPE is a measure of how much a deep learning model has learned about each example in a given training batch.
The LPE can be obtained by finding the difference between the per-example-loss before and after an optimization step, as shown in the following code block:
loss_per_example = loss_fn(model.predict(x_batch))
loss = loss_per_example.mean()
loss.backward()
model.optimize_step() # update model based on gradient
loss_per_example_after_update = loss_fn(model.predict(x_batch))
learning_per_example = loss_per_example_after_update - loss_per_example
For the training example of index, i,
the value, learning_per_example[i],
tells us exactly how much better the model
has got for this example after the optimization step:
- If
learning_per_example[i]is positive the model has got worse at predicting this example (the loss for this example increased after the training step). - If
learning_per_example[i]is negative the model has got better at predicting this example (the loss for this example decreased after the training step). - If
learning_per_example[i] == 0the model’s ability to predict this example has not changed (the loss for this example has not changed).
LPE, takes into account batch effects (e.g. conflicting examples that prevent the model learning, or the inverse), as well as optimizer settings and state (e.g. momentum, clipping, learning rate, etc.).
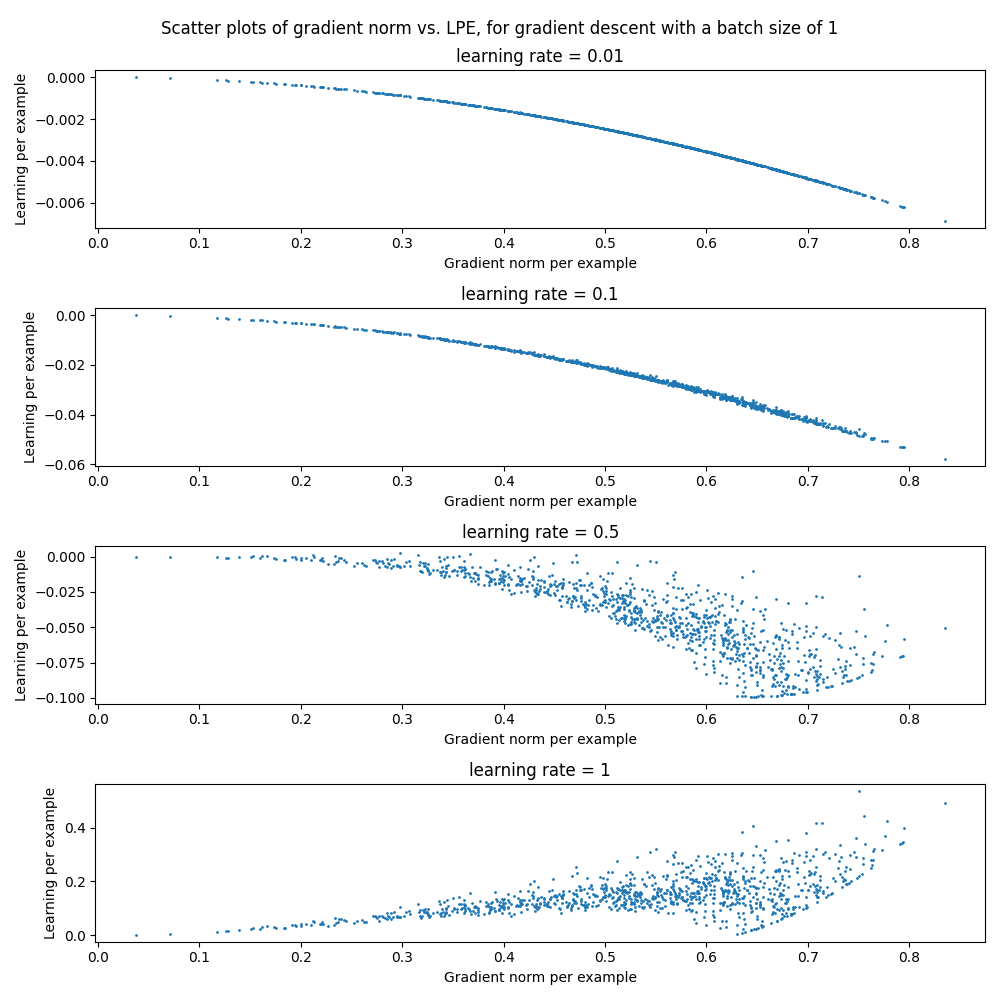
A common measure of example importance is the gradient norm. The following plot shows how the gradient norm values are good predictors of LSE, (for this particular, dummy example), but that it can become a poorer predictor when the optimization environment changes (in this case the learning rate). The LSE shows how much the model would actually learn, for a given gradient norm. Note that when the learning rate is too high, the model actually gets worse (positive values in the lowest plot); and the gradient norm does not predict this.
Uses:
- A metric to evaluate model training
- A metric to evaluate data quality
- A measure of example importance, for curriculum learning. E.g. easy to learn samples, and difficult to learn samples
Notes:
- When
batch_size > 1there may be batch effects. These can be estimated/combatted by repeated measurements, either with repeated measurements and random shuffling, or exhaustively running through the permutations (infeasible for most but tiny toy examples). - Fixed-time LPE, (LPE_ft), involves resetting the model and optimizer state to how they were before the optimize step, to enable computing the LPE value over the whole dataset at a fixed point in the model’s training.
- In-training LPE, (LPE_it), is when the model and optimizer state are not reset, meaning the LPE is being computed at a different time in the model’s training for each example. In this case, the LPE values that are close together in time are likely to be more comparible than values further apart in time. And the relative / normalized / ordinal value of the LPE may also be more useful here.
- LPE_ft is more expensive/slow, since it requires restoring the model/optimizer state after each update.
- LPE_it is straightforward to compute, but costs an extra inference step.
Pseudocode for fixed-time LPE code block:
fixed_model = make_copy(model)
fixed_optimizer = make_copy(optimizer)
loss_per_example = loss_fn(model.predict(x_batch))
loss = loss_per_example.mean()
loss.backward()
optimizer.step() # update model based on gradient
loss_per_example_after_update = loss_fn(model.predict(x_batch))
learning_per_example = loss_per_example_after_update - loss_per_example
# Restore the model and optimizer state
model = make_copy(fixed_model)
optimizer = make_copy(optimizer)
After conducting a literature search, I was unable to find any examples of this concept, which suggests that it might be a novel idea. If you have come across any relevant literature or examples of this concept, please share them in the comments below / via email. Further research is necessary to confirm the originality of this concept. If something comes up, I’ll edit this post.