Wider nets without the memory cost
(Work in progress)
Wider artificial neural networks require more memory to train, run and store. Randomly permuted parameters (RPP) is proposed as a method for widening nets without increasing memory consumption. Using RPP, network width can be multiplied by $k$, and instead of the parameter count, $q$, increasing multiplicatively to $ \bar{q} = q * k $, it either stays the same, or increases additively to $\bar{q} \approx q + k$, if biases are not reused. RPP works by using a hidden weights matrix, from which a larger, permuted weights matrix, is created. The elements of the permuted weights matrix are pointers to elements of the hidden weights matrix, and each element of the hidden weights matrix appears $k$ times in the permuted weights matrix. Preliminary experiments demonstrate empirically that this method is promising.
Method
A standard neural network layer can be written as:
\(\boldsymbol{h} = g(\boldsymbol{x}W)\)
Using RPP, each column of $W$ is randomly permuted $k$ times, to create $k$ new columns in weights matrix, $W_p$.
\([h_0 ... h_{k*n-1}] = g([x_0 ... x_{m-1}] \begin{bmatrix} w_{p_{0,0,0},0} & w_{p_{0,0,1}, 1} & ... & w_{p_{0,0,n-1}, n-1} & ... & w_{p_{k-1,0,0},0} & w_{p_{k-1,0,1}, 1} & ... & w_{p_{k-1,0,n-1}, n-1} \\ w_{p_{0,1,0},0} & w_{p_{0,1,1}, 1} & ... & w_{p_{0,1,n-1}, n-1} & ... & w_{p_{k-1,1,0},0} & w_{p_{k-1,1,1}, 1} & ... & w_{p_{k-1,1,n-1}, n-1}\\ \\ w_{p_{0,m-1,0},0} & w_{p_{0,m-1,1}, 1} & ... & w_{p_{0,m-1,n-1}, n-1} & ... & w_{p_{k-1,m-1,0},0} & w_{p_{k-1,m-1,1}, 1} & ... & w_{p_{k-1,m-1,n-1}, n-1}\\ \end{bmatrix})\)
Where $p_{h,i,j}$ is an element of $P$, the random permutation tensor used to index $W$. The values of $P$ are needed for both forward and back propagation, and should stay constant for a given network layer, but $P$ does not need to be stored in memory, because it can be generated by a deterministic random algorithm. ($P$ is constrained such that the indices correspond to column-wise permutations as described above.) Alternatively, a single $P$ can be stored in memory, and used for multiple layers (this works for layers that have the same shaped weight matrix), in which case the number of model parameters for a network of depth $d$ would become, $\bar{p} = mnd + mnk$, instead of $\bar{p} = mnd*k$ if the layers were widened the standard way.
Preliminary results
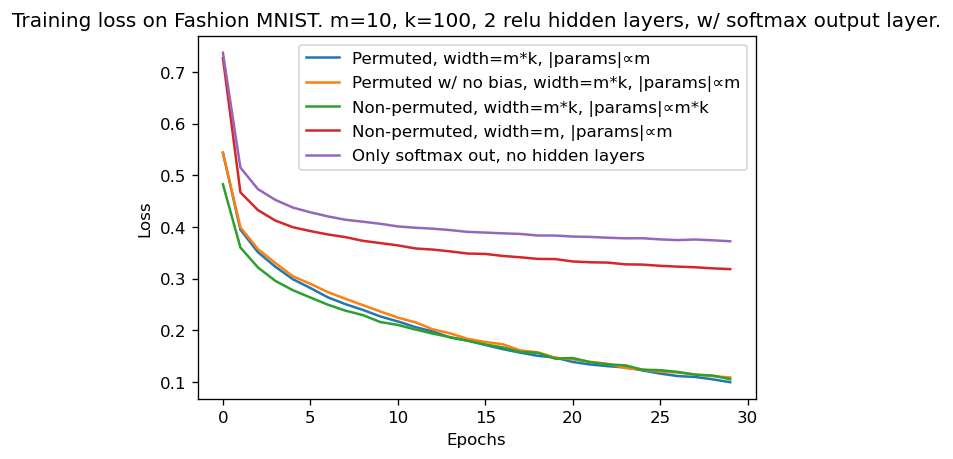
The above plot shows RPP layers performing as well as layers with 100 times more parameters.